明日方舟抽奖概率太低,《明日方舟》作为一款热门的手机游戏,拥有众多忠实玩家,但近期许多玩家纷纷反映,游戏中的抽奖概率较低,让许多人感到心痛。针对这一现象,我们不妨从《明日方舟》抽卡机制入手,探讨其中的一些细节,为玩家们分享一些经验。
从明日方舟抽卡机制开始的些微探索经验分享
明日方舟的抽卡机制还是很好理解的,正常2%,超过50次每次增加2%,简单来说就是一种给游戏公司有个收入保底,然后在保证玩家平均能抽到一定次数后提高概率,以提高非酋玩家的抽卡体验。
对这种形式,抽卡的概率是非常容易计算的,完全可以写出抽X次出六星的概率,然后计算均值,简单来说,对每一次抽卡时的概率,第1次到第50次概率为0.02,第51次为0.04,按等差数列以此类推,在第100次是概率为1。
值得注意的是,上述的概率指的都是在之前没有抽中的条件下的概率,即条件概率,所以我们可以表示为如下形式:
P(X_{n}|\bar{X_{n-1}}\bar{X_{n-2}}...\bar{X_{1}})
这么写不太严谨,不过意思就是前n-1次全部没有抽中的条件下第n次抽中的概率。由于求第n次抽卡抽中的概率要求前n-1次不能抽中,所以事件组中只有前面全部没有抽中这个事件的概率非零(稍微有点绕),那么根据全概率公式,应该有如下等式成立:
P(X_{n}) = P(X_{n}|\bar{X_{n-1}}\bar{X_{n-2}}...\bar{X_{1}})P(\bar{X_{n-1}}\bar{X_{n-2}}...\bar{X_{1}})
而由于每一次抽卡的概率相互独立(你这一次抽中和没有抽中对下一次抽卡没有影响,不考虑有的垃圾游戏公司搞事的情况),所以对上式右边的第二项可以拆成如下形式:
P(\bar{X_{n-1}}\bar{X_{n-2}}...\bar{X_{1}}) = \prod_{i=1}^{n-1}P(\bar{X_{i}}) = \prod_{i=1}^{n-1}(1-P(X_{i}))
这就非常容易计算了,直接贴上Matlab代码。第一行清除一下乱七八糟的工作区就很舒服:
clc;clear;
% 设置条件概率
p = zeros(1, 100);
for i = 1 : 50
p(i) = 0.02;
end
for i = 51 : 100
p(i) = p(i-1) + 0.02;
end
% 设置前n-1次没有抽中,第n次抽卡抽中的概率
count = ones(1, 100);
count(1) = p(1);
for i = 2 : 100
for j = 1 : i-1
count(i) = count(i) * (1- p(j));
end
count(i) = count(i) * p(i);
end
% 求均值
for i = 1 : 100
count(i) = count(i) * i;
end
sumx = sum(count);代码用Matlab打开就能用,求解出来均值是34.5946,这个数字应该已经很多人算过了,以上工作也是别人算过很久了的,这里推导一遍也仅仅是兴趣使然。不过讲道理,无论怎么考虑这些抽卡机制,我这种非酋就是非酋,不存在抽到想要的角色的......
那么下面我们探索一些更有意思的东西,以下问题由我朋友提出。(真的不是无中生友)
类似明日方舟这种概率只增不减,抽中直接变成最低,这显然是游戏公司为了你抽中以后尽快把你的抽中概率降到最低,减少你的愉悦时间而设计的,但对于单机游戏,通常只需要平衡素材出货率,把玩家的游戏时间平衡在一个合理范围就行。
以下纯属探索,咱也不知道这是啥,咱也不敢问。推理着玩玩,不保证出结果
我们不妨假设最开始的时候抽中概率为0,每次抽中,则再下一次抽中概率减去1%,每次没有抽中,再下一次抽中概率加上1%,当然,最低不能低于0%,最高不能高于100%。
可能有人会觉得这么说有点难理解,我们举个例子。第1次抽中的概率为0,所以第1次必定没有抽中,那么现在第2次抽卡时抽中概率为1%,不抽中概率为99%;现在抽第2发,如果抽中,那么第3次抽中概率又变成0%,如果没有抽中,则第3次抽中概率为2%。
直观上理解,连续不中的次数越多,抽中概率越高;连续抽中的次数越多,抽中概率越低。这非常符合单机游戏里对素材爆率的需求,而且每次提升和每次下降的幅度相同,我们相信最终概率会在50%上下波动,这里的概率指的是每次抽中的条件概率,即当前状态下,下一次抽中的概率。
要提炼出这种东西的模型不容易,但编一个模拟上述抽奖过程的程序还是非常简单的。
clc;clear;
N = 1e6; % 总的抽奖次数
delta = 0.01; % 每次变化的概率,本次设置为1%
p = zeros(1,N); % 初始化概率表,用于记录每次抽中的条件概率
for i = 2 : N
x = rand; % 生成随机数,用于判断是否抽中
if x < p(i-1) % 若抽中
p(i) = max(0, p(i-1) - delta);
else % 若没有抽中
p(i) = min(1, p(i-1) + delta);
end
end
plot(p); % 绘图贴上跑出来的图片,横坐标是抽卡次数,纵坐标是在第n-1个状态下第n次抽卡的概率:
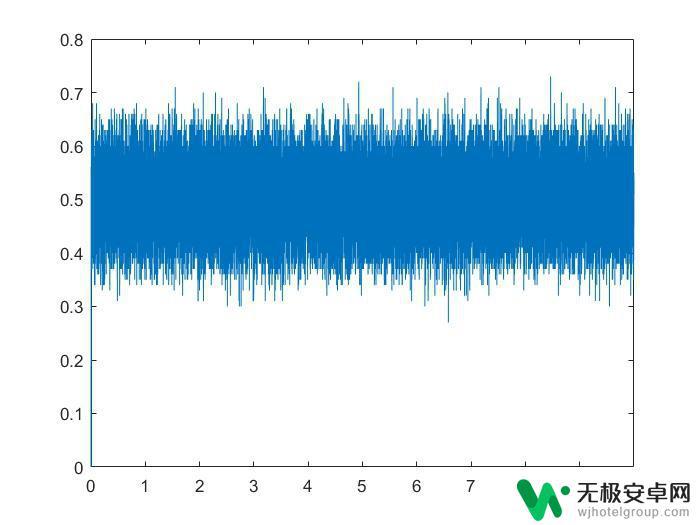 仿真次数为1M时每次抽中的概率的曲线
仿真次数为1M时每次抽中的概率的曲线有点近似我们的想象,但又好像不太一样。虽然确实是在50%周围浮动,但浮动有上下20%,稍微有点大。看起来这个概率没有往50%靠近的趋势,反而和马尔科夫链有点类似,但马尔科夫链是无记忆的,或者最多n-1阶有记忆,但这里的情况应该是和之前所有状态都有关系。这显然不应是一个马尔科夫链。
我们注意到每个点的概率在50%的上下20%波动,而上图看起来就很有噪声的感觉(学通信学久了。看啥都是高斯白噪声),那么为了看看这个概率的值满足什么分布,我们不妨将概率的直方图统计出来,在这里我们进行了1M次的仿真模拟,统计的是每个概率出现的频率:
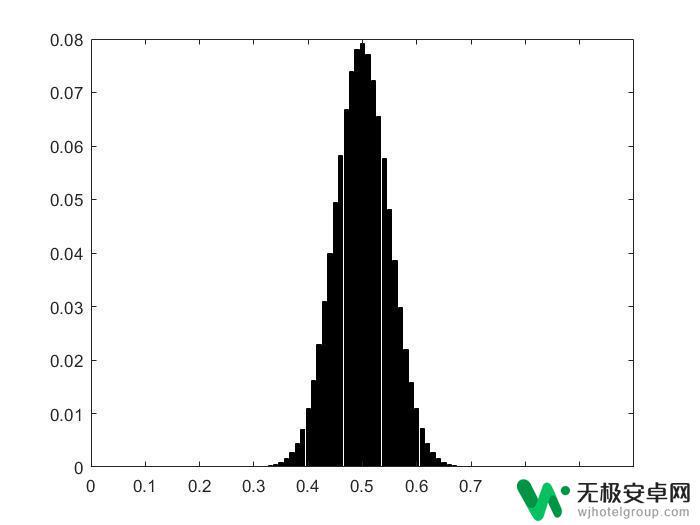 仿真次数为1M时各概率的出现频率
仿真次数为1M时各概率的出现频率这就很有意思了,有点高斯分布的味道了。显然这不可能是一个高斯分布,因为高斯分布的取值可以到正负无穷,但这里的概率的取值是有限值。如果真的近似符合高斯分布,那么我们很容易想到这可能是因为中心极限定理导致的,但中心极限定理要求每一个事件独立,所以这应该也无法使用中心极限定理(神秘)。
感觉不知道这是个啥啊,专业的玩不动还不如玩一点花里胡哨的。
首先想到的是调整步进的值,在1%的时候和50%的时候显然是不一样的,而显然当步进的值越小,能够分得的直方图的条(我真不记得这叫啥了)的数量也会变多。当然,当步进值变小时,总的仿真次数也需要增加,否则每个点不一定有足够多的点形成直方图,我们不妨设计平均每个概率能有10000个点来统计出直方图。
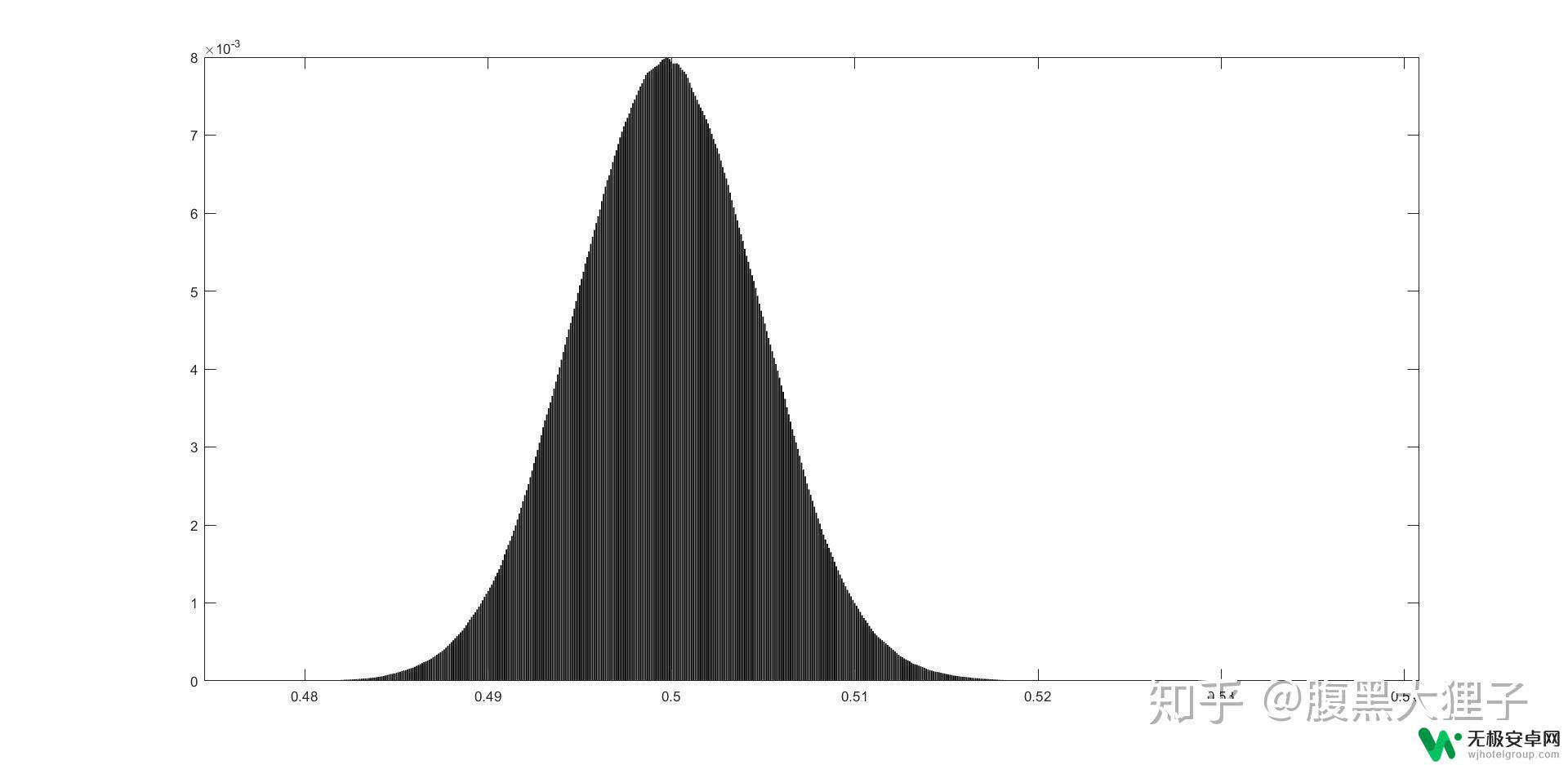 概率为0.01%,统计100M次的统计直方图
概率为0.01%,统计100M次的统计直方图似乎还是能有一个类似于高斯分布的东西,但咱也没用假设检验证明,也就估计个大概。
感觉这玩意儿还能多研究一下,不过目前随机过程和信息论都忘得差不多了,感觉补一补再滚回来继续研究会能得到更多的结果。
最后算一算这玩意儿的均值,程序接上文的程序:
hist = zeros(1, 1/delta + 1);
for i = 1 : N
x = floor(p(i) / delta) + 1;
hist(x) = hist(x) + 1;
end
hist = hist / N;
x = 0 : delta : 1;
bar(x, hist,'k');
xlim([0 1])
count = x .* hist;
sumx = sum(count);在步进1%,算1M仿真次数时,求得均值为0.4996,还是很接近50%的,至少基本能肯定,这里的概率的概率的概率密度其均值是0.5了。
滚去复习吧......
在明日方舟的抽卡机制中,玩家可以选择不同的抽卡方式以及挑战活动关卡来获得更好的抽奖概率。此外,还可以通过收集游戏内的物品和资源来换取更多的抽卡机会。不要气馁,多尝试不同的方法,提升自己的抽奖概率吧!










